Smart traders won’t execute a trade without measuring its potential risk or reward. Quickly calculating the implied volatility using a theoretical pricing model can give traders the opportunity to better analyze a particular position before executing.
QuikStrike’s Simple Option Calculator allows you to select the type of trade you plan to execute (call, put or straddle), customize the pricing model inputs (strike price, future price, days to expiration and interest rate) and calculate the theoretical price (given a volatility value) or find the implied volatility (given an option price). You’ll notice that when you click “Calc Vol” or “Calc Price”, the associated Greek values are also calculated.
How does it work?
In many ways, the Simple Option Calculator is just that, simple. However, it’s important to go through the correct process when calculating the implied volatility of a particular position.
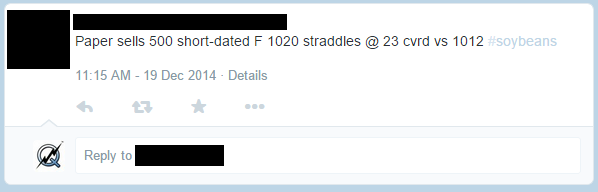
Let’s look at a trade recently posted on Twitter:
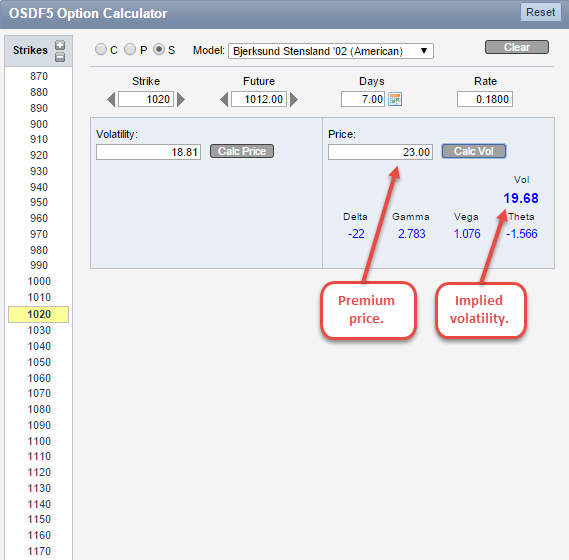
From this tweet, we can ascertain that Paper sold a short-dated January soybean straddle for $23 with a 1020 strike price and 1012 future price. While we don’t know the exact DTE and interest rate, we can surmise that since the trade was posted on 12/19, there were roughly 7 DTE (although QuikStrike users will have this information automatically populated as part of the calculator’s pre-population of initial pricing values) and we can use the current interest rate in QuikStrike. In this instance, we were given the premium price, so all we have to do is plug in the variables to find the implied volatility.
Now that we have the implied volatility, take that to the Trade Builder to create the trade and review in more detail. Quickly calculating the implied volatility makes the Simple Option Calculator an extremely valuable tool. However, we are not done on this page, we still have to evaluate the Greeks. Since the trade we are reviewing is a short straddle, the Greeks would take on the opposite sign as seen above. Below is a breakdown of the Greeks for this position:
- Delta: All calls have a positive delta while all puts have a negative delta. The delta of a straddle can move from positive to negative to neutral. As the underlying price changes, the delta values will do the same. The 22 value represents how much the straddle price will change when the underlying moves. The call and put move by their respective delta values. The straddle moves as a summed combination of the two.
- Gamma: The rate of change of the delta is known as the gamma. For every one point change in the underlying, gamma represents the number of deltas gained or lost. With a gamma value of 2.783, for every one point change in the underlying, the delta will gain or lose 2.783 deltas.
- Vega: As the option decays, volatility may change, as well as the theoretical value of the option. The vega value represents how the theoretical value of the option changes for each percentage point change in volatility. In this particular position, the theoretical value of the option will change 1.076 with each percentage point change in volatility.
- Theta: An option will lose value as time decreases, and the rate of this change is known as the theta. In this example, the theoretical value of the option will lose value at the rate of 1.566 for each day the position moves toward expiration.
(Note: QuikStrike has Greek help in the QS.EDU section which takes in to account all the scale factors we use for each product)
Does this post answer any questions you may have about the Simple Option Calculator? Are you ready to calculate the implied volatility of your position? Let us know your thoughts. Comment below or send us an email at [email protected]. We hope you are enjoying the holiday season!